√70以上 30 60 90 triangle area formula 498845-30-60-90 triangle theorem formula
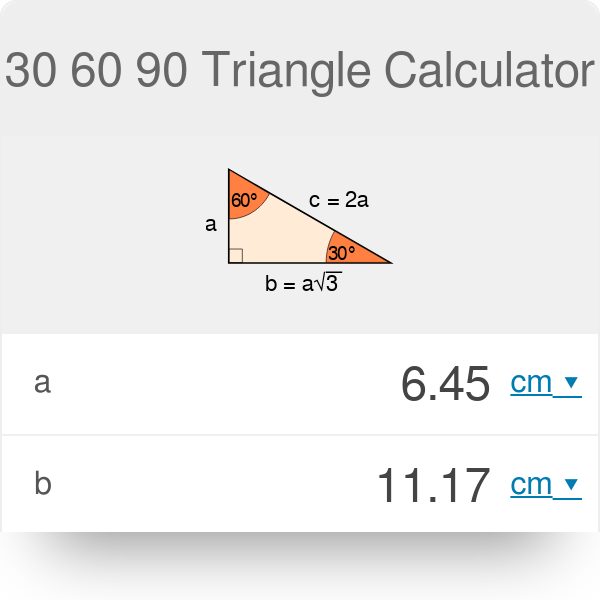
30 60 90 Triangle Calculator Formula Rules
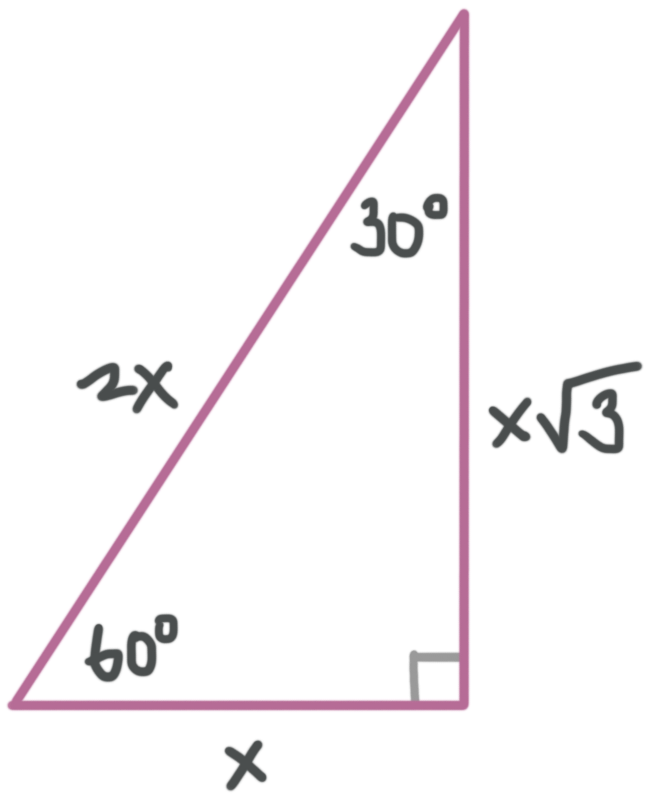
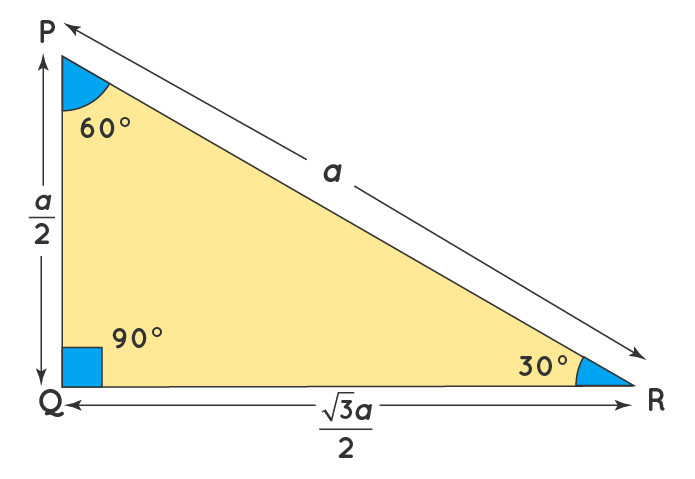
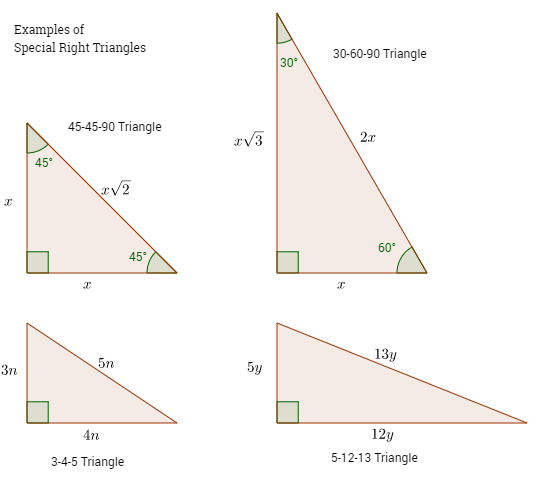
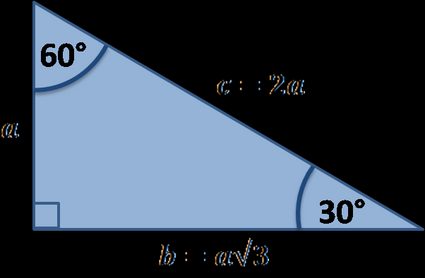
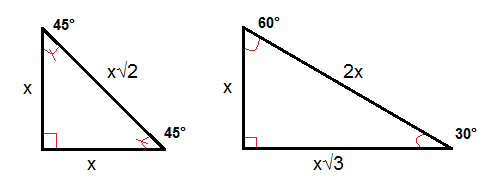
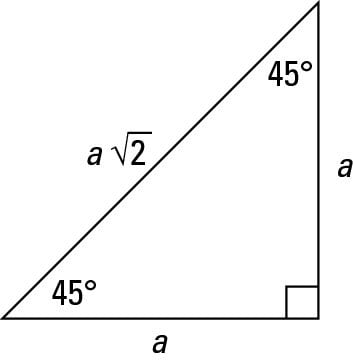
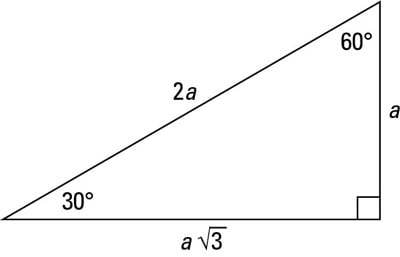
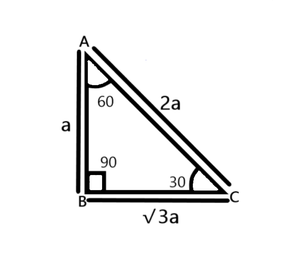
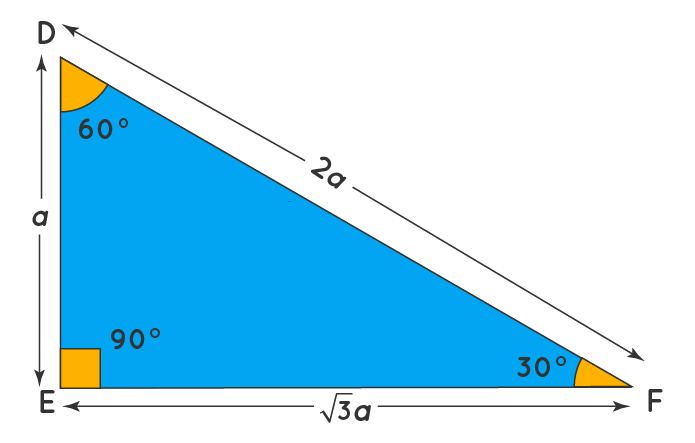
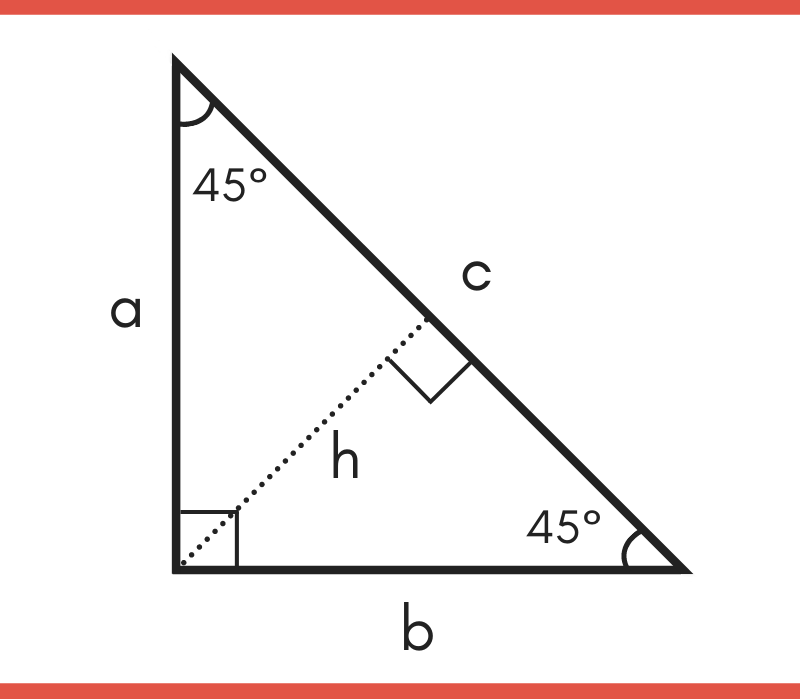
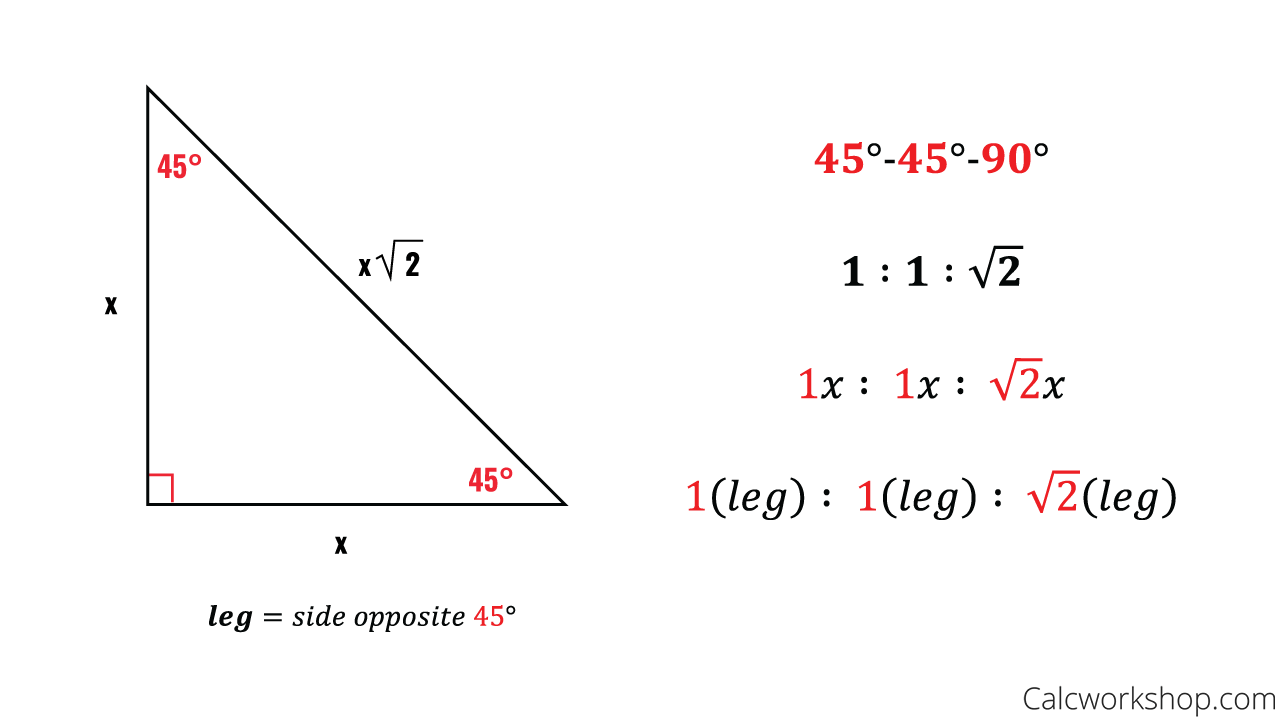
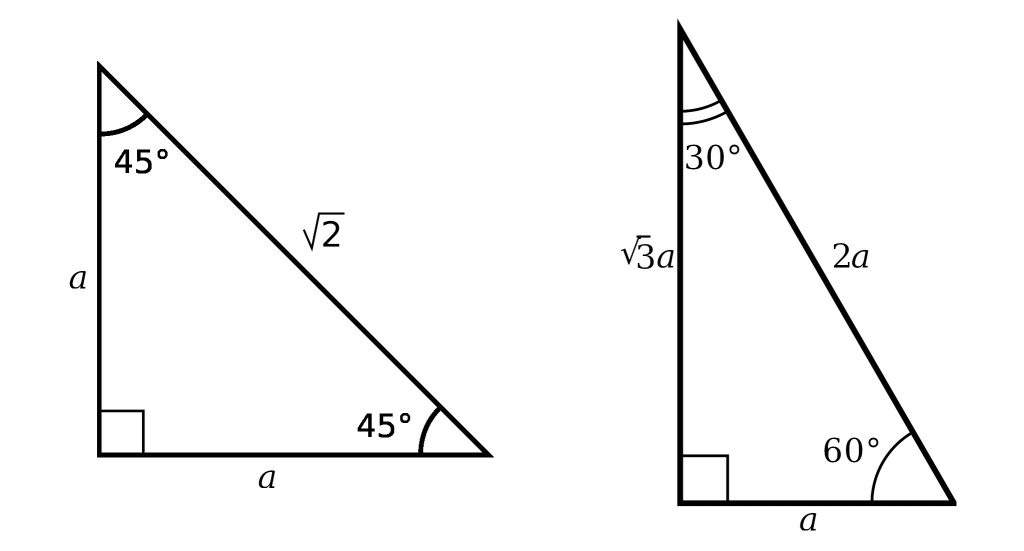
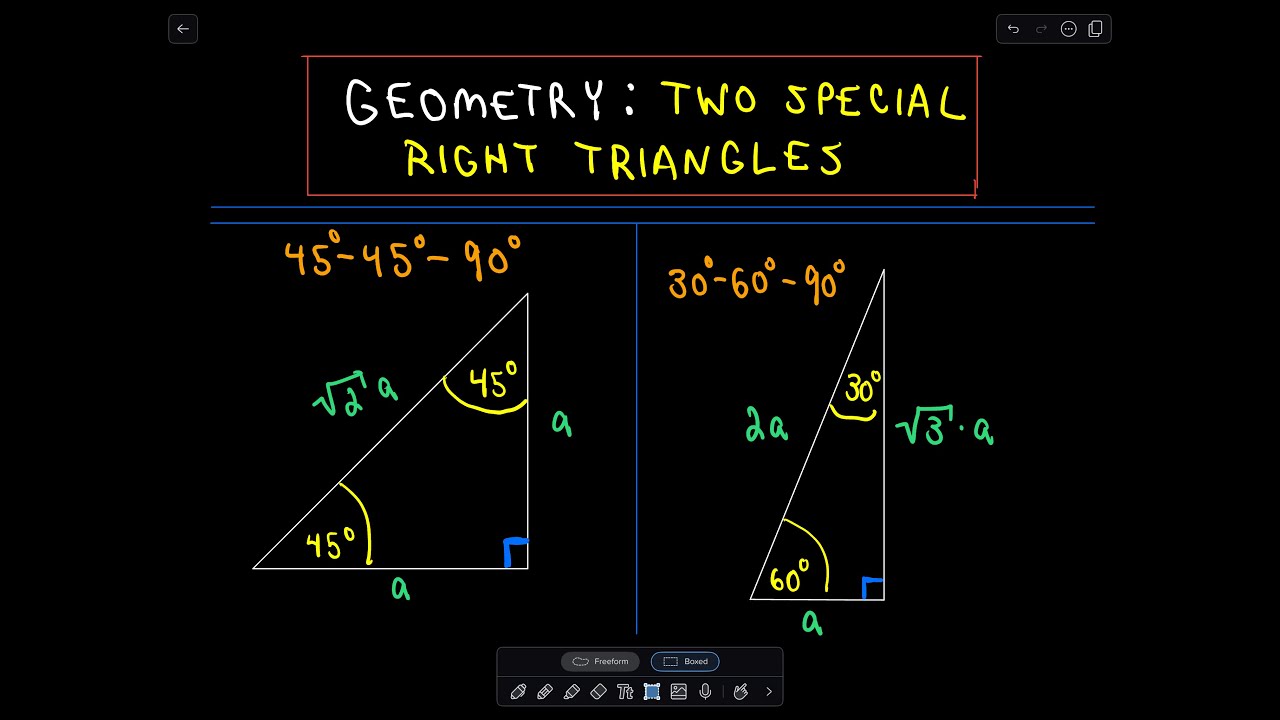
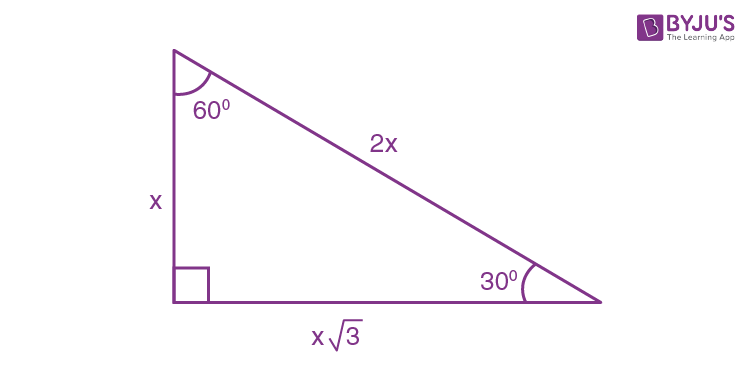
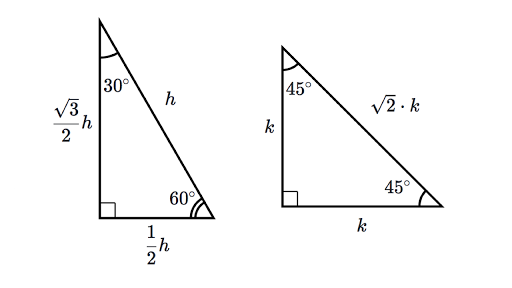
The 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sides30 60 90 triangle formula Assume that the shorter leg of a 30 60 90 triangle is equal to a Then the second leg is equal to a√3 the hypotenuse is 2a the area is equal to a²√3/2 the perimeter equals a (3 √3) The formulas are quite easy, but what's the math behind them?
30-60-90 triangle theorem formula
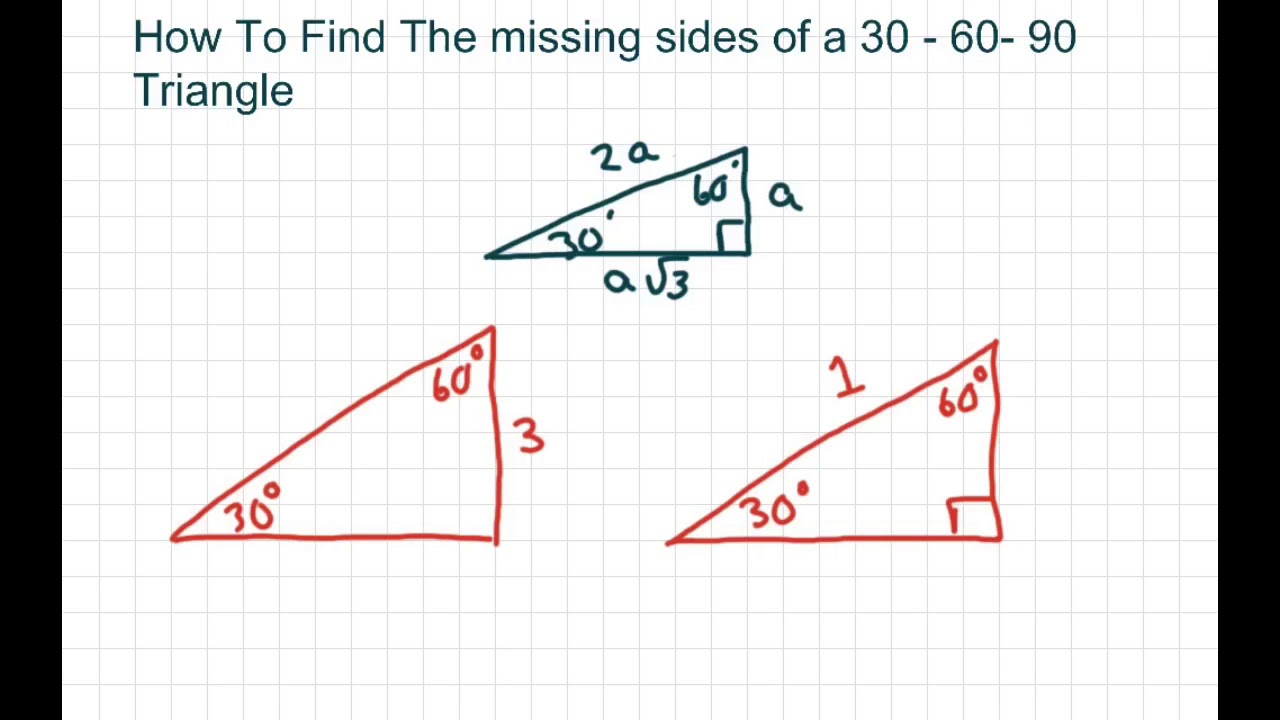
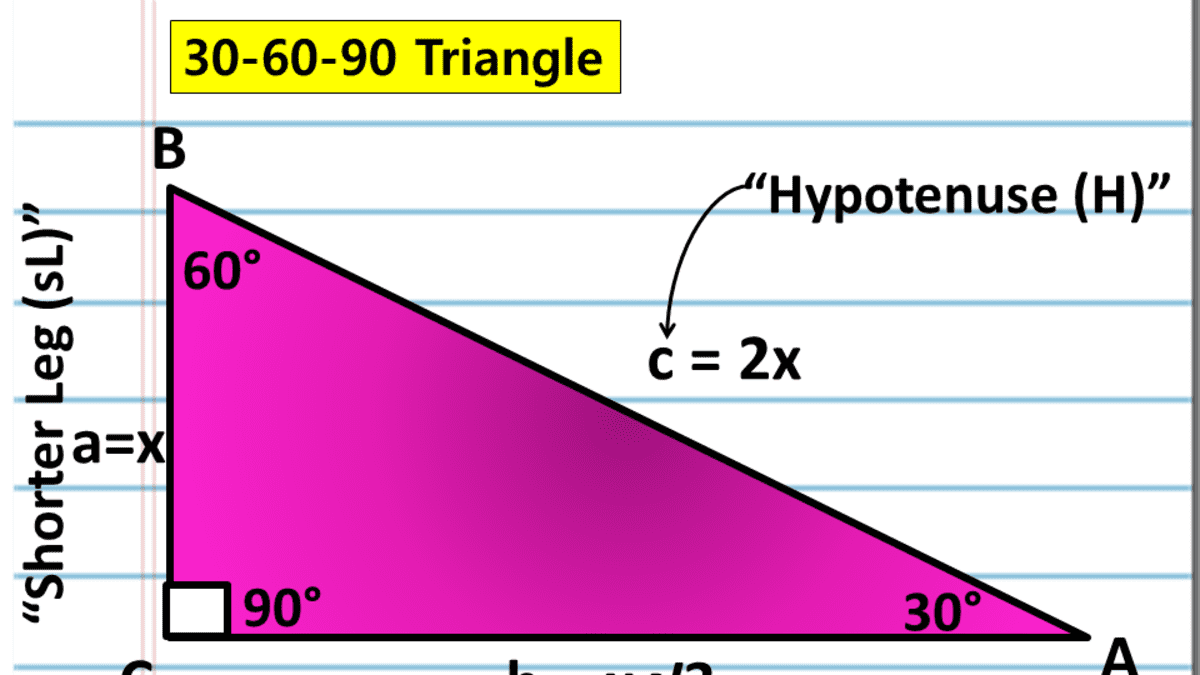
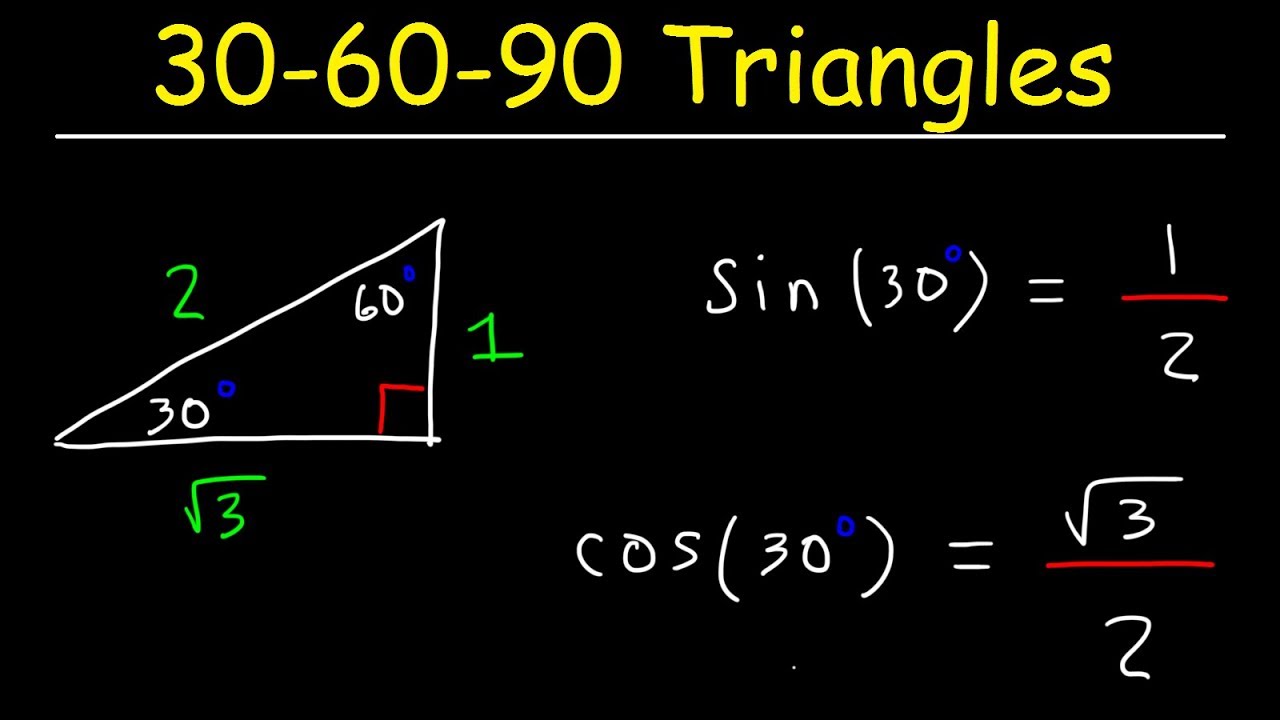
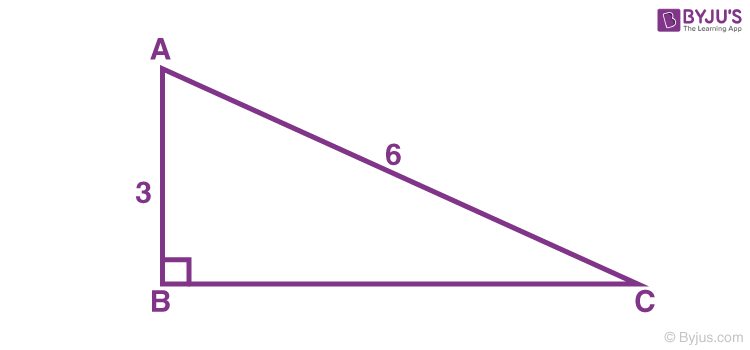
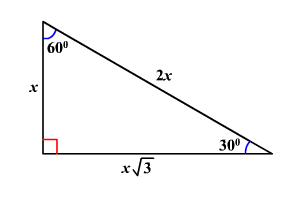
30-60-90 triangle theorem formula-30 60 90 Triangles E1 Find the hypotenuse of a triangle with a short side of 3 units Hypotenuse= Step 1 Use the formula 2*s Step 2 2*3 =6 units E2 Find the long side of a thirty sixty ninty triangle with a short side of 3 units Long leg = Step 1 This means that the ratio of the lengths of the shortest side to the hypotenuse of any right triangle is 12 Therefore, If a triangle is a right triangle, the ratio of the sides (short leglong leghypotenuse) is 1√32 Hereof, what is the formula of right angle triangle?

30 60 90 Triangle Theorem Ratio Formula Video
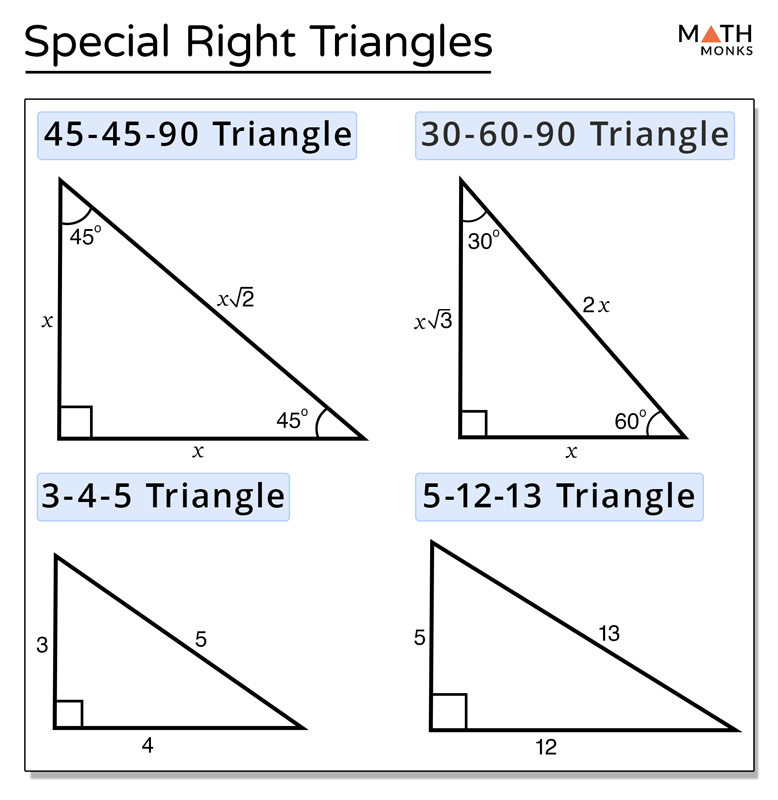
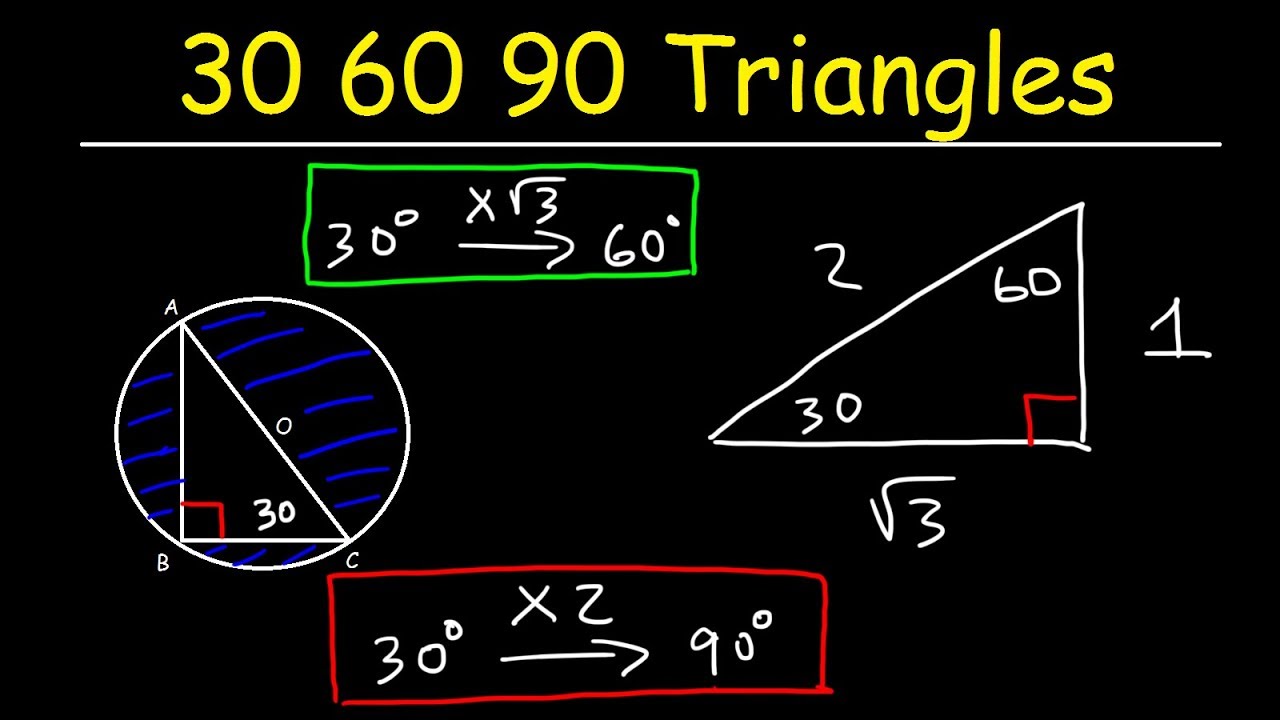
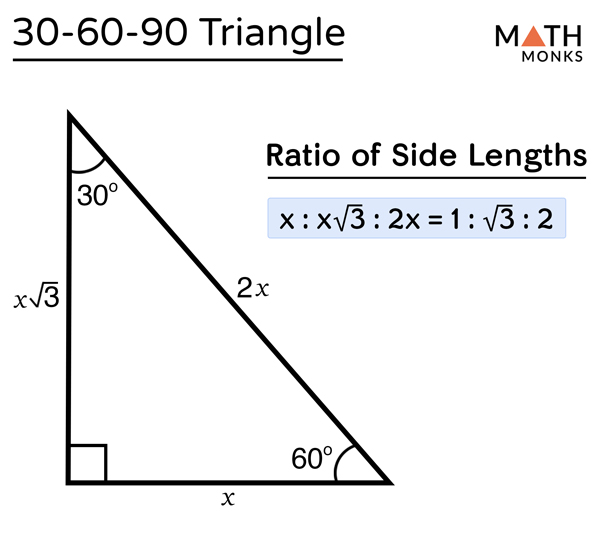
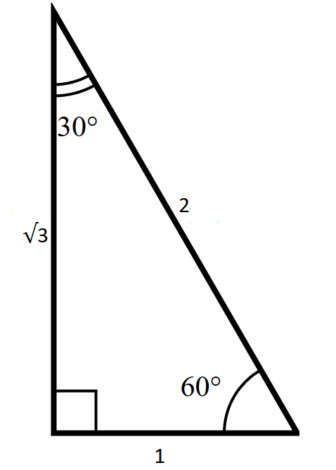
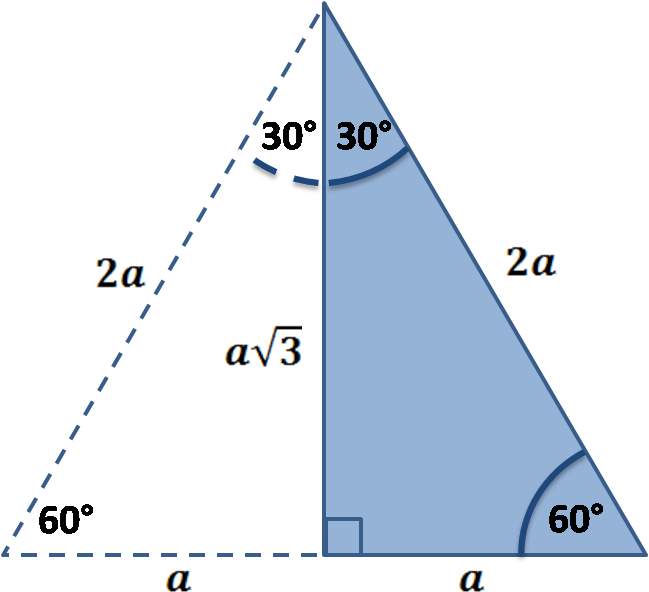
The triangle is also a right triangle The Formulas of the Given that X is the 30 60 90 Right Triangle Calculator Short Side a Input one number of input area LongThere are two special right triangles with angles measures as 45, 45, 90 degrees and 30, 60, 90 degrees The sides of these triangles are in particular ratios and are known as Pythagorean triplets Let us learn the special right triangles formulas along with a few solved examplesHere is the proof that in a 30°60°90° triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90° triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60° (Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30° angles
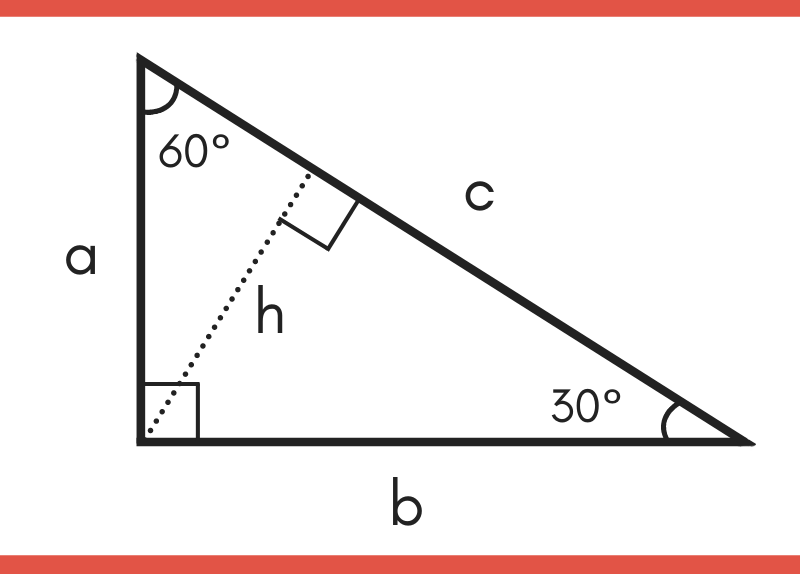
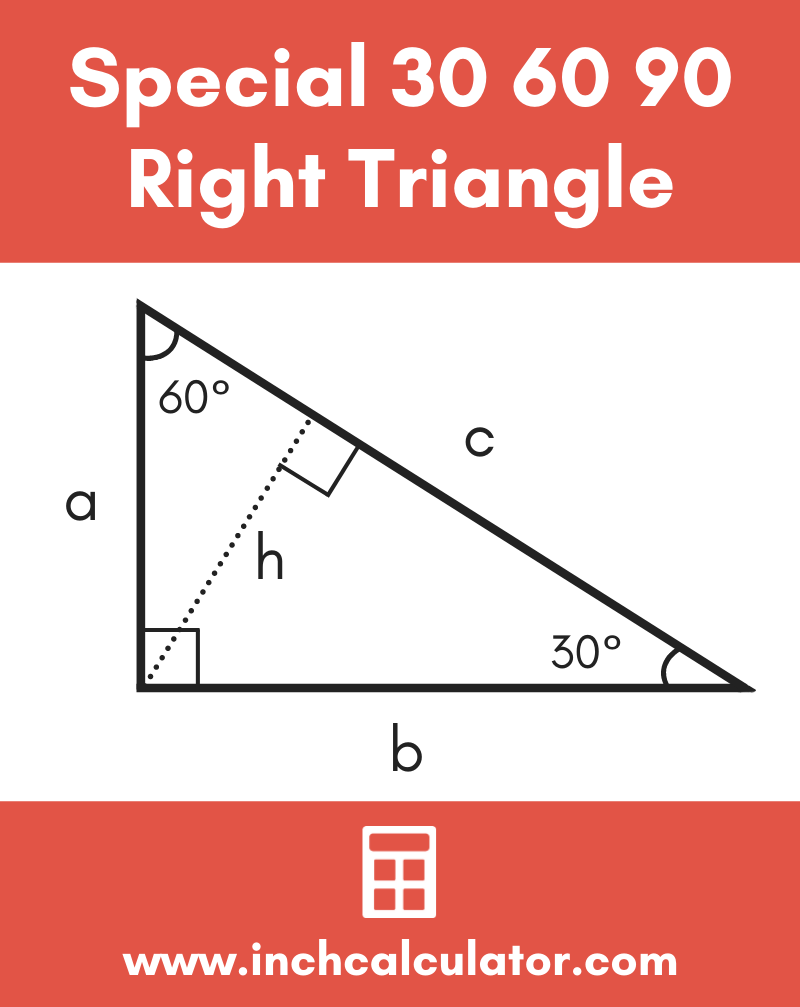
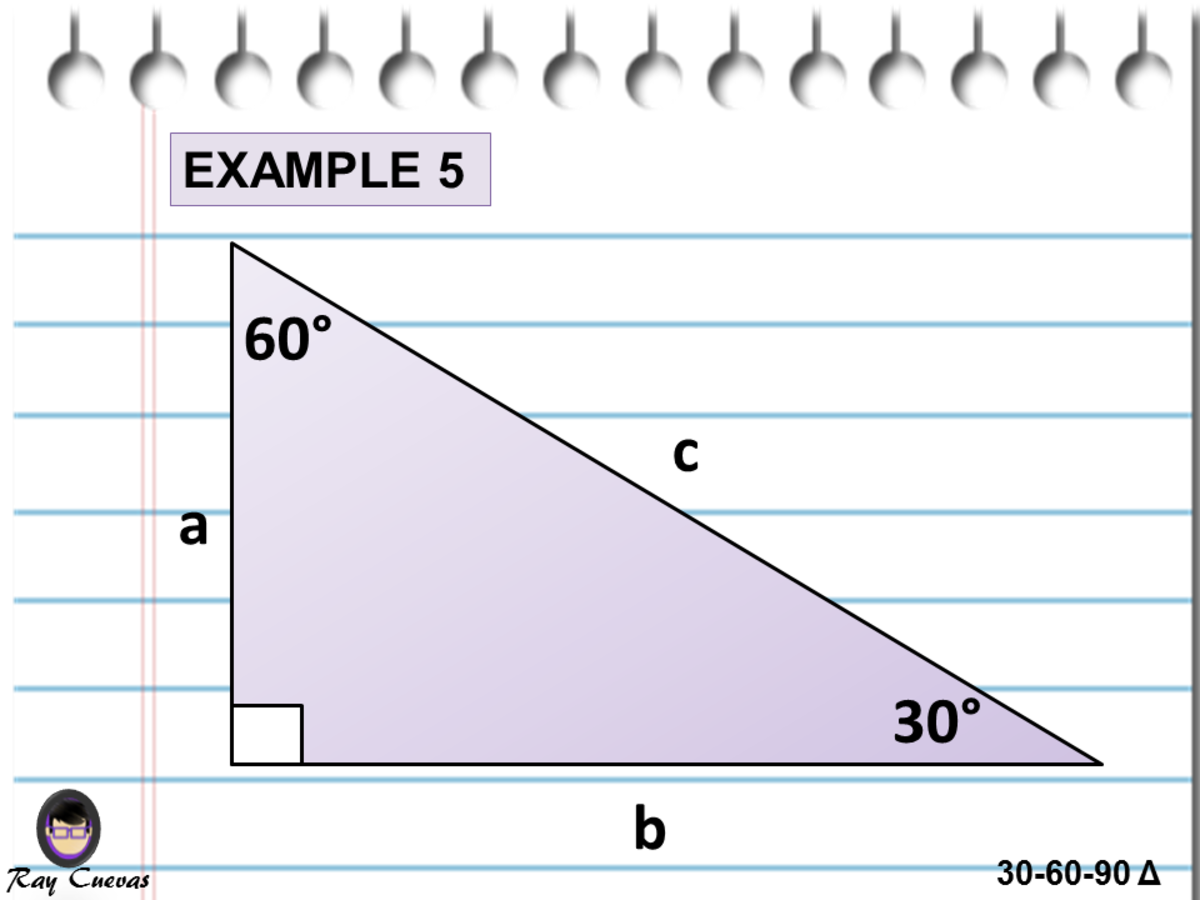
Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangle You know a triangle is half an equilateral triangle, so the base is half of the hypotenuse L #b=L/2# You can use now Pythagoras theorem and calculate the height #h=sqrt(b^2 L^2)= sqrt(L^2/4 L^2)=sqrt(3/4L^2)=L/2sqrt(3)=bsqrt(3)# So we can determine the area only knowing one of the edges 1) If we know #L#A triangle is a right triangle with angle measures of 30º
30-60-90 triangle theorem formulaのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
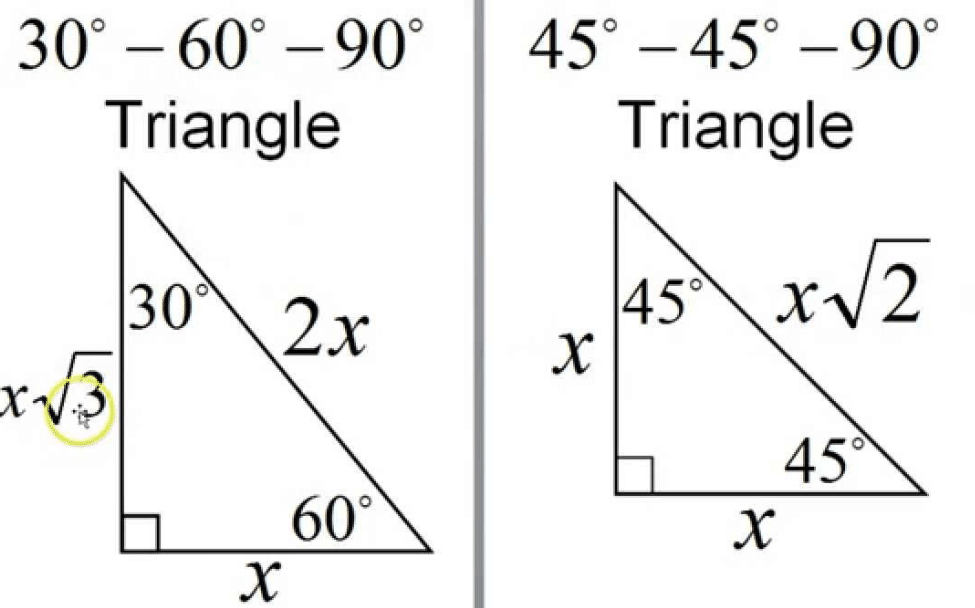 |  |  |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「30-60-90 triangle theorem formula」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
By Rich Zwelling, Apex GMAT Instructor Date 14th January, 21 As promised, we will now connect the triangle to the equilateral triangle, specifically its area There is a formula for the area of an equilateral triangle as it relates to the length of its side s, and it is as follows But more likely than not for the GMAT, you'll need to understand how this formula isApp description 30 60 90 triangle calculation formula Area = 05 * Long side * Short side;
Incoming Term: 30 60 90 triangle area formula, 30 60 90 triangle formula, 30-60-90 triangle finding sides, 30 60 90 triangle formulas, 30-60-90 triangle formula for short leg, 30-60-90 triangle formula for long leg, 30 60 90 triangle formula examples, 30 60 90 triangle formula chart, 30-60-90 triangle theorem formula, 30 60 90 triangle hypotenuse formula,




コメント
コメントを投稿